Unique color gradient fill quadrangle
Posted: Sat Nov 28, 2015 2:05 am
In Topic: http://bb.donnay-software.com/donnay/vi ... 8&start=20 Auge_Ohr I brought the image:
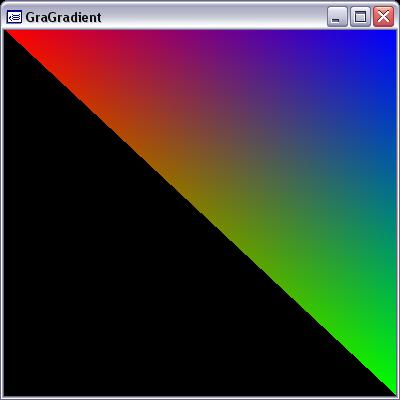
I try to apply this function to a gradient color quadrangle

for the vertices of which are known coordinates X,Y,Z, and Z coordinate of the displayed color.
Here's a snippet of my program:
[/size]
Maybe it is possible to give an example of a source code program running?
I think I made a mess with the order of traversal of triangles in a quadrilateral or/and the order of traversal of vertices in triangles...
PS
1. The method which I expect the quadrilateral coordinates of the vertices in this case is not essential. The debug program would be most convenient to specify the vertex coordinates directly in the program or in the dialogue.
2. Actually, I really need to learn how to paint a gradient color krayneyi at least 9 contiguous quadrangles. In the simplest case, they may be located in both the number keys on the numeric keypad.
I try to apply this function to a gradient color quadrangle

for the vertices of which are known coordinates X,Y,Z, and Z coordinate of the displayed color.
Here's a snippet of my program:
Code: Select all
***** The calculation of the coordinates of the vertices of the quadrilateral ***************
X1 := X0 + Ax * mMinGrInt1 * COS( aOpSc[mNOpSc,2] * 3.14159265358979323846 / 180 )
Y1 := Y0 - Ay * mMinGrInt1 * SIN( aOpSc[mNOpSc,2] * 3.14159265358979323846 / 180 )
Z1 := mInf1
X2 := X0 + Ax * mMaxGrInt2 * COS( aOpSc[mNOpSc,2] * 3.14159265358979323846 / 180 )
Y2 := Y0 - Ay * mMaxGrInt2 * SIN( aOpSc[mNOpSc,2] * 3.14159265358979323846 / 180 )
Z2 := mInf2
X3 := X0 + Ax * mMinGrInt3 * COS( aOpSc[mNOpSc+1,2] * 3.14159265358979323846 / 180 )
Y3 := Y0 - Ay * mMinGrInt3 * SIN( aOpSc[mNOpSc+1,2] * 3.14159265358979323846 / 180 )
Z3 := mInf3
X4 := X0 + Ax * mMaxGrInt4 * COS( aOpSc[mNOpSc+1,2] * 3.14159265358979323846 / 180 )
Y4 := Y0 - Ay * mMaxGrInt4 * SIN( aOpSc[mNOpSc+1,2] * 3.14159265358979323846 / 180 )
Z4 := mInf4
******************************************************************************************
***** Calculation of coordinates of the intersection of the diagonals of the quadrilateral space: (x, y, z)
******************************************************************************************
***** В прямоугольнике:
***** --------------------------------
***** |2 4|
***** | |
***** | |
***** | 0 |
***** | |
***** | |
***** |1 3|
***** --------------------------------
***** Two diagonals:
***** 1st connects vertices 1-4;
***** 2nd connects vertices 2-3.
***** Accordingly canonical equations of the 1st and 2nd diagonals are of the form:
***** (x-x1)/(x4-x1)=(y-y1)/(y4-y1)=(z-z1)/(z4-z1)
***** (x-x2)/(x3-x2)=(y-y2)/(y3-y2)=(z-z2)/(z3-z2)
***** We write these equations in the form:
***** (x-x1)/p1=(y-y1)/q1=(z-z1)/r1
***** (x-x2)/p2=(y-y2)/q2=(z-z2)/r2
***** где:
***** p1=x4-x1, q1=y4-y1, r1=z4-z1
***** p2=x3-x2, q2=y3-y2, r2=z3-z2
***** Then the coordinates of the intersection point of the diagonals (x, y, z) would be:
***** x=(x1*q1*p2-x2*q2*p1-y1*p1*p2+y2*p1*p2)/(q1*p2-q2*p1)
***** y=(y1*p1*q2-y2*p2*q1-x1*q1*q2+x2*q1*q2)/(p1*q2-p2*q1)
***** z=(z1*q1*r2-z2*q2*r1-y1*r1*r2+y2*r1*r2)/(q1*r2-q2*r1)
******************************************************************************************
p1=x4-x1;q1=y4-y1;r1=z4-z1
p2=x3-x2;q2=y3-y2;r2=z3-z2
x=(x1*q1*p2-x2*q2*p1-y1*p1*p2+y2*p1*p2)/(q1*p2-q2*p1)
y=(y1*p1*q2-y2*p2*q1-x1*q1*q2+x2*q1*q2)/(p1*q2-p2*q1)
z=(z1*q1*r2-z2*q2*r1-y1*r1*r2+y2*r1*r2)/(q1*r2-q2*r1)
IF mFlagView
********* Dimensioning gradient fill color for all triangles *****************
ma := 127
mb := 127
mc := 127
mU := 0
mV := 120
mW := 240
****** Color 1st vertex of the quadrangle
mColor1 = ABS(INT( mDeltaSpectr + (360-mDeltaSpectr) * (mInf1 - mIntInfMin) / (mIntInfMax-mIntInfMin) ))
R := INT( ma * (1 + COS( ( mColor1 + mU ) * 3.14159265358979323846 / 180 ) ) )
G := INT( mb * (1 + COS( ( mColor1 + mV ) * 3.14159265358979323846 / 180 ) ) )
B := INT( mc * (1 + COS( ( mColor1 + mW ) * 3.14159265358979323846 / 180 ) ) )
fColor1 := GraMakeRGBColor({ R, G, B })
****** Color 2nd vertex of the quadrilateral
mColor2 = ABS(INT( mDeltaSpectr + (360-mDeltaSpectr) * (mInf2 - mIntInfMin) / (mIntInfMax-mIntInfMin) ))
R := INT( ma * (1 + COS( ( mColor2 + mU ) * 3.14159265358979323846 / 180 ) ) )
G := INT( mb * (1 + COS( ( mColor2 + mV ) * 3.14159265358979323846 / 180 ) ) )
B := INT( mc * (1 + COS( ( mColor2 + mW ) * 3.14159265358979323846 / 180 ) ) )
fColor2 := GraMakeRGBColor({ R, G, B })
****** The color of the top of the third quadrilateral
mColor3 = ABS(INT( mDeltaSpectr + (360-mDeltaSpectr) * (mInf3 - mIntInfMin) / (mIntInfMax-mIntInfMin) ))
R := INT( ma * (1 + COS( ( mColor3 + mU ) * 3.14159265358979323846 / 180 ) ) )
G := INT( mb * (1 + COS( ( mColor3 + mV ) * 3.14159265358979323846 / 180 ) ) )
B := INT( mc * (1 + COS( ( mColor3 + mW ) * 3.14159265358979323846 / 180 ) ) )
fColor3 := GraMakeRGBColor({ R, G, B })
****** The color of the 4th vertex of the quadrilateral
mColor4 = ABS(INT( mDeltaSpectr + (360-mDeltaSpectr) * (mInf4 - mIntInfMin) / (mIntInfMax-mIntInfMin) ))
R := INT( ma * (1 + COS( ( mColor2 + mU ) * 3.14159265358979323846 / 180 ) ) )
G := INT( mb * (1 + COS( ( mColor2 + mV ) * 3.14159265358979323846 / 180 ) ) )
B := INT( mc * (1 + COS( ( mColor2 + mW ) * 3.14159265358979323846 / 180 ) ) )
fColor4 := GraMakeRGBColor({ R, G, B })
****** The color of the points of intersection of the diagonals of the quadrilateral
mColor = ABS(INT( mDeltaSpectr + (360-mDeltaSpectr) * (Z - mIntInfMin) / (mIntInfMax-mIntInfMin) ))
R := INT( ma * (1 + COS( ( mColor + mU ) * 3.14159265358979323846 / 180 ) ) )
G := INT( mb * (1 + COS( ( mColor + mV ) * 3.14159265358979323846 / 180 ) ) )
B := INT( mc * (1 + COS( ( mColor + mW ) * 3.14159265358979323846 / 180 ) ) )
fColor := GraMakeRGBColor({ R, G, B })
***** Blend the four triangles in the rectangle formed by the parties and the halves of the diagonals
aClrs := {} // 1-й треугольник: 0, 1, 2
AADD(aClrs, fColor1);AADD(aClrs, fColor2);AADD(aClrs, fColor)
GraGradient(oPS, {X1,Y1}, {{X2,Y2}, {X,Y}}, aClrs, GRA_GRADIENT_TRIANGLE)
aClrs := {} // 2-й треугольник: 0, 2, 4
AADD(aClrs, fColor2);AADD(aClrs, fColor4);AADD(aClrs, fColor)
GraGradient(oPS, {X2,Y2}, {{X4,Y4}, {X,Y}}, aClrs, GRA_GRADIENT_TRIANGLE)
aClrs := {} // 3-й треугольник: 0, 3, 4
AADD(aClrs, fColor4);AADD(aClrs, fColor3);AADD(aClrs, fColor)
GraGradient(oPS, {X4,Y4}, {{X3,Y3}, {X,Y}}, aClrs, GRA_GRADIENT_TRIANGLE)
aClrs := {} // 4-й треугольник: 0, 1, 3
AADD(aClrs, fColor3);AADD(aClrs, fColor1);AADD(aClrs, fColor)
GraGradient(oPS, {X3,Y3}, {{X1,Y1}, {X,Y}}, aClrs, GRA_GRADIENT_TRIANGLE)
ENDIF
Maybe it is possible to give an example of a source code program running?
I think I made a mess with the order of traversal of triangles in a quadrilateral or/and the order of traversal of vertices in triangles...
PS
1. The method which I expect the quadrilateral coordinates of the vertices in this case is not essential. The debug program would be most convenient to specify the vertex coordinates directly in the program or in the dialogue.
2. Actually, I really need to learn how to paint a gradient color krayneyi at least 9 contiguous quadrangles. In the simplest case, they may be located in both the number keys on the numeric keypad.

















